When I first learned inventory planning the safety stock calculation math was rather simple. On top of the cycle stock (expected demand during lead time) I would add a percentage or a number of days (or more likely weeks). If the lead time was 2 weeks I might carry 3 or 4 weeks. I soon learned that demand for some inventory items is more volatile than for others, and some suppliers less reliable than others. I’d rather have too much then not enough, and I’d never gotten in trouble for having a little too much.
So since all items and situations are different I started using some statistics; (average demand * lead time) + (one sided Z factor * demand standard deviation) for the target inventory level; a little better approach.
Here’s another safety stock calculation from Inventory Management Review;
Safety Stock:
{Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2)}.
(note ^2 means ‘square’)
Reorder Point:
Average Lead Time*Average Demand + Safety Stock.
Over at QuickMBA ; To calculate the safety stock, first calculate the standard loss function, designated as L(z). This function is dependent on the values of the desired fill rate f, the demand μ and its standard deviation σ , the time between orders p, and the replenishment lead time l : L(z) = ( 1 – f ) µ p / σ ( p + l )1/2. Once L(z) is known, z can be found in a look-up table and the safety stock can be calculated by:
Safety Stock = z σ ( p + l )1/2
Here’s a new one recently published by Kent Linford in the APICS Magazine Nov/Dec 2006.
SS = √ [( σFE)2 x (LTI/FI)beta + ( σLT)2 x D2] x Z x (FI/OCI)beta
Where:
SS = safety stock
FE = forecast error
LT = lead time interval
FI = forecast interval (pick a beta between 0.5 and 0.7)
D = average demand during lead time
Z = normal distribution service factor based on desired service level
OCI = order cycle interval
Dave Piasecki at InventoryOps.com uses;
safety stock = (standard deviation)*(service factor)*(lead-time factor)*(order cycle factor)*(forecast-to-mean-demand factor)
And so too does Joannès Vermorel, and a nice spreadsheet example.
Michel Baudin makes an interesting comment on safety stock in an article titled Beware of Formulas.

Accounting Explained has this one …
Safety Stock = (Maximum Daily Usage − Average Daily Usage) × Lead Time
Any questions? Got any other versions? What formula do you use?
Larry Loucka

123 thoughts on “Safety Stock Calculation”
What formula do you use if demand is Weibull or exponentiall distributed? Or discreet? Just use the formulas which assume normally distributed products?
Great question Thom. I assume what you are trying to get at is what to do when the quantity (not lead time) probability distribution has a long tail. Well, let’s think about what safety stock is trying to do – carry enough extra inventory to protect supply from higher than usual demand. Maybe a place to start is to decide how much insurance you want to buy. That is, how much of the probability on the high side do use. If you want 95% service level, then find the value for P(0.95) * lead time and use that for your target inventory level.
Or, simulate the demand and use trial and error to set safety stocks.
Owen is the store’s manager of a supplying company on the east. Last year demand for motors was 1,500 per year, which is estimated to go up by 10% this year. The price of a motor was 50 dollars ans has gone up by 15% this year. Ordering cost is $75 per order and the carrying cost is 12% per motor.
Determine the a) Economic Order quantity (EOQ) using the fomulae
b) EOQ graphically
c) The number of orders per year
Help…………….
EOQ = 67
Try http://www.ultimatecalculators.com/economic_order_quantity_calculator.html
# of orders = 1650/67
For a graphical tool try
http://office.microsoft.com/en-001/templates/basic-eoq-model-TC010370172.aspx
Did you think that it is not correct to use standard deviation to calculate the Safety Stock?
Because periods with demand below the average will increase SS according the formula!!!
But we do not need SS at all if demand below the average. Stock = Lead Time Demand is enough for such periods without any SS.
Only periods with demand bigger than the average should be considered for SS calculation.
So in your opinion, should all days where 0 are consumed be considered as a value when determining the ADU?
Silly Question Time.
In a food distribution network where the structure is supply – warehouse – store – consumer we have an expectation that as the number of stores increases the buffer stock at warehouse increases. However, we also feel that the average stock held in the warehouse per store should fall.
Is there a simplified formula that can support this theory.
We are looking at the transition to a multi tier network with slow moving goods held nationally in a single stock holding point with faster moving lines being held regionally. The hope is that this should allow us to have a lower overall stock holding.
Any help / support / guidance would be most welcome as senior managers are looking for more than gut feel and instinct before making what is for us a large capital outlay on a full network review.
Thanks in advance
Paul
Paul, Maybe the Square Root Law of Inventory is what you are looking for.
One or two cautions about centralizing the slow movers. How do you define ‘slow’? Low volume steady eddy items moved to a single stock point will be trouble. And how do you plan on dealing with seasonal products?
Larry
Jonas,
You’re right. Intermittent, right-skewed demand patterns have an effect on safety stock. Central Limit Theorem says that a demand distribution tends toward normal as lead time increases, but it may not apply in your example of dramatic skewness and a relatively short lead time.
Interestingly, our proprietary analysis of your demand data found a better option than bootstrapping, since bootstrapping has some disadvantages.
Here are some other safety-stock factors you will need to know:
• Lead-time variation, and its pattern.
• How willing are you to expedite? If you can’t (or can’t afford to) expedite, you will need more safety stock.
• Is your 98% service-level target a fill rate, or a probability of no stockouts? A fill rate requires less safety stock.
• Does unfulfilled demand become past-due backlog, or is it cancelled? Past-due backlog requires more safety stock.
As you observed, reorder quantity, or its corresponding replenishment interval, is also a factor. As replenishment interval gets increasingly longer or shorter than lead time, less safety stock is needed.
I ran your data through our safety-stock analysis. If my estimates on the missing factors are correct – and they probably aren’t! – there’s about a 25% probability of a unit sitting on the shelf longer than 60 days and requiring the re-test you described.
If you can provide me with the data I’m missing, I can give you reliable answers on your inventory item’s safety stock, shelf-life risk and other important expected performance measures: http://topdownleansystems.com/contact.php.
David McPhetrige
TopDown Lean Systems
Dear Lawrence
I have been looking through the formulas and the comments below, but didn’t really seem to find an answer to my problems. I am currently working on a project where the calculation of safety stock at our US facility is very important (funny enough):) but I’m having troubles, due to the demand variation.
The current situation:
Based on historical daily demand the distribution is much right-skewed (actually ressembles a negative exponential distribution) with a high level of intermittent demand. To illustrate som of the data:
Total data size = 426 days
Days with demand 0 = 57,74% Average Daily demand= 1,08
1 = 19,72% St. deviation = 1,99
2 = 8,22% Review periode = continuous review
3 = 6,57% Leadtime = 9 days (is for a fixed Quantity of 12)
4 = 2,35% Service Level = 98%
5 = 1,17% St. Dev of lead time is precently unknown
6 = 0,70%
7 = 0,47%
8 = 1,64%
9 = 0,23%
10 = 0,23%
11 = 0,47%
12 = 0,23%
13 = 0,00%
14 = 0,23%
Due to the intermittent demand pattern I have found assistance in in the Bootstrap method inspired by http://www.werc.org/assets/1/workflow_staging/Publications/809.PDF but I am very uncertain whether this method gives my what I need. From conducting af 5000 sample Bootstrap calculation i get an Average Demand during lead of 10,76, and the 98th percentile of the distribution results in a target inventory level of 29, which would indicate a SS of 19. I am however not comfortable with this calculation! Is there anyway you, based on this limited information, could advise me whether I am on the correct path, or if there are any other ways to you knowledge on how to determine SS of intermittent demand?
Furthermore I this is correct do you have any ideas on how to incorporate:
1) the fixed reorder/replenishment quantity of 12pcs? (the bootstrap method does to my knowledge asssume reorder qunatity of 1
2) What if the products have a limited lifetime? In my case the products can only be stored for 60 days without before they need to go back to production and be tested.
I know this is a lot, but I really hope you can aid or guide me 🙂
Best Regards
Jonas Rasmussen
Hello Sir/Madam,
I would like to impliment safety stock at suppliers end. Major suppliers are from Europe, Asia and USA. Request to please guide me on this. Also my goal is minimize lead time of the supplier as well.
Regards,
Shrikant
Hello Shrikant,
If you have your demand history and forecast why don’t you calculate the safety stock and ask your suppliers to do the same?
Suggest reading: Inventory Management Explained: A focus on Forecasting, Lot Sizing, Safety Stock, and Ordering Systems by David J. Piasecki.
Lawrence Loucka
Paul, think about time fences and reaction time. For example, can you make a change to your demand forecast +/- 25% due twelve months from now? Can your supplier go +/- 5% in 15 days. How big is your ‘frozen’ zone – the next 3 months? Can you make demand changes in month 4? So for safety stock how much will actual demand vary in your frozen zone? This is the safety stock you need. Don’t need safety stock for month 12. OK?
What I am struggling with is how to adequately figure that reaction time if I have suppliers that are producing and delivering in a regular frequency i.e. weekly, biweekly. I have some suppliers that have pretty long lead times and so if I use the full mfg and transportation lead time the safety stocks (minimum we want them to have on site) can get pretty high. If I have a supplier that has a 3 month lead time but receives a rolling 12 mo forecast and is replenishing inventory on our site weekly would we use a week or 3 months? This could obviously mean they are producing more than they deliver and holding stock and then just shipping to us weekly or they are producing a new batch every week. Appreciate your suggestions.
Thanks
Working on a VMI program with suppliers and evaluating minimum inventory to be maintained. How do you figure lead time for calculating appropriate inventory levels (min, max, etc.) for a supplier that is making to a forecast you provide them? Do you use the lead time it would take for a discrete PO being issued to delivery to your dock, just the delivery time from the supplier to you, or something else.
Thanks
Paul, if supplier is making to forecast why do you need safety stock? Usually because your forecast is wrong and you need to have the supplier make a change that’s not reflected in the forecast. So then, as you suggest, you would use the “reaction time”. You could include in the lead time your time to recognize the actual demand deviation from the plan/forecast, plus the time to communicate the new demand, plus the supplier’s lead time (manufacturing and transportation time for example).
Dear Lawrence, thanks for your response. Regarding the breakdowns, if we look into the past data, than few months back this was the major issue. And the breakdowns were like punching tool break down or machine breakdown. These issues are already taken care. Regarding capacity, supplier is having enough capacity in accordance with the demand.
Presently issues with supplier are that whatever supplier is making them are they are supplying on same or next day. So in case there is any issue in production due to any reason or lot get rejected by Final SQC or delay is delivery, than this directly impacts the production at our OEM resulting in miss order. Our experience in the past was so bad that the as a first step we would like to define the safety stock so that chance of order miss get minimized. Once the supplier process get streamlined & confidence get built in supplies this buffer stock qty will be reduced to zero (as keeping inventory is just like keeping you money ideal). Another reason for keeping safety stock is that presently this supplier is supplying 80% of total requirement. Development of alternate source is already is in progress.
Regarding keeping inventory at our end than we are planning for having 3 days advance planning result in 3 days inventory at our OEM end. Need your inputs on this also.
Regarding order placing, we raised the week’s requirement & supplier supplies material distributed throughout the week. Target was to complete week order by the end of week. (This can be from 4 days to 6 days or some times even supply by end of week day due to which our OEM struggles in production) And if talk about the lead time than 3~4 days is the production lead time for component & 1 day is travelling time.
Thanks…..
Hi All…
I’m new to this forum, so first i give my small intro….basically a mech. graduate & having a exp in manufacturing industries. Presently working as a Black Belt to improve Customer service level in SCM.
In regard of my project i need few inputs from the experts as I’m new to SCM.
My issue is that our supplies to customer are hitted by non performance of our one of supplies. Main reason why our supplier is not able to cater the demand is due to some breakdowns etc…. issues. Another thing is that he has no Safety stock of finished goods material with them to take care of any such breakdown or uncertainty. We have asked him to keep safety, but the safety stock figure given to him is not scientifically calculated. Before further getting into other issues with supplier I want to define safety stock at his end which is based on some scientific calculations.
Pl help is calculating the desired safety stock…..
Thanks in Advance….
abhishek
Adhishek, lean thinking says that inventory is muda (Japanese for waste). When we put safety stock in place we cover up the causes. Your supplier has breakdowns and is unreliable. One approach is to add inventory safety stock, the other approach is to go to your supplier and try to help reduce breakdowns. Maybe the supplier needs preventive maintenance. Maybe the supplier needs some capital?
If you must put safety stock in place right now then you need to have some history on the supplier’s variation in lead time (including breakdown duration and frequency). Safety Stock is used to disconnect your customers, your operation, and your supplier. Safety Stock can help deal with variation in demand and supply. It can be helpful to split these two. Some of your safety stock can be for buffering changes in your customer orders, some can be for changes in supplier leadtime. Find out all the steps from needing materials from your supplier until those materials are available: reorder trigger, create purchase requisition, approval, create purchase order, notify supplier, negotiate delivery date, manufacture, transportation, receiving, inspection, putaway, requisition, etc. all these take time and have variation in time. If you have some history or can make some estimates then your safety stock can be 1 or 2 standard deviations on the high side of the lead time variation.
If the supplier can’t carry safety stock, can you? Once you have some safety stock you might then be able to get the supplier to do the same.
Rajesh,
My advice is to contact Kent Linford via the email link on his name, above. Also, you can contact Dave Piasecki directly through his InventoryOps Website. I know Kent will answer your email, and I’m sure Dave will, too. I’m confident that their explanations of their formulas will be better than mine.
We have several white papers that discuss forecast error, order cycle (replenishment interval) and the other factors that affect safety stock, service level, inventory performance and expediting costs at http://www.topdownleansystems.com/white.htm.
David McPhetrige
TopDown Lean Systems, LLC
Dave and Lawrence,
Thanks – this is a good compilation of formulae which covers most usage.
I am trying to build the order cycle factor into my safety stock calculation, and just wanted to quickly check on a couple of things with you.
– I like Dave Piasecki’s formula, but unsure how exactly it is used – if a company does monthly forecasts and uses a 2 year rolling forecast and foreceast accuracy in its error calculations, would the forecast period by 1 month, or 2 years? And the order cycle itself is the time between orders, or is it the number of orders per time period? i.e. if a company orders an SKU every 15 days, would this factor be 0.5 months or 2 times a month? the latter seems more intuitive, since more times you order, the lesser will be the safety stock needed….Would be great to see an example here to explain the logic
– In the Kent Linford formula, how is FI and OCI defined? Is it similar to the above?
– Is there any other method in this case?
Thanks!
Rajesh
Verrami,
We can help you with your safety-stock analysis, and we can handle your large number of inventory items. It’s what we do. I invite you to contact me through our Website, at http://topdownleansystems.com/contact.php.
David McPhetrige
TopDown Lean Systems, LLC
Dave and Lawrence
Thanks for the replies! I am hesistant to use forecast numbers as accuracy has been traditionally low. The reason for monte-carlo/bootstrapping approach is that, as you rightly noted, its very hard to characterize demand distribution for parts I am dealing with. Most are right-skewed. I used another method where I feed LTD to a statistical package and it fits a distribution. I can calculate LTD from CDF and subtract average LTD to get SS estimate. Its a manual method and I can’t do it for the number of products I am dealing with.
I’m looking into applying these methods with a mix of historical demand (actual) and some future (predicted).
Verrami,
You’re right, historical demand is the best source for the random demand variation that safety stock is intended to cover. The ideal is actual customer-requested demand from sales-order history, not inventory shipment transactions. Of course, it’s very important to isolate the random-variation component of historical-demand variation. If you don’t, then your safety stock will “double up” on variation that’s already been predicted in your forecast: Trend, seasonality and predictable special causes (promotions, sales, etc.).
Also, as your latest post suggests, it’s important to use the distribution model that’s the best fit for the historical demand distribution. We select best fit from an array of distributions, and we have found that these typically work better and are more practical than bootstrapping or Monte Carlo methods.
One of the advantages of using historical demand is that it is daily. Daily data provides more data points, and is not susceptible to the netting of peaks and valleys that occurs when demand is summarized into monthly buckets.
Larry’s comment on forecast error brings up an important point: Forecast error can indicate chronic forecast bias, and safety stock should be adjusted by the bias. (Well, actually, the first course of action with chronic bias is to stop biasing the forecast. Sometimes, however, this is easier said than done.)
In your latest post, you propose using standard deviation of demand to determine safety stock. I think your post answers your question, since you said that you’re using bootstrap or Monte Carlo. I assume you’re using these techniques because the historical demand distributions are skewed (demand is nearly always right-skewed), not normal. If you were to use a typical standard-deviation calculation for safety stock, that standard deviation would assume normality, and this would not represent the historical distribution. Although the central limit theorem can come into play over the course of the lead time, I’ve found that it often does not apply in the real world of skewed distributions, intermittent demand and shorter lead times.
I’ve found that these factors also have a significant impact on safety stock, service-level achievement, expediting and inventory performance: Lead-time variation, replenishment interval (MOQ, EOQ, package size, etc.), probability of past-due backlog vs. cancellation of unfulfilled demand, and ease/difficulty of expediting. See our white paper, “Service Level and Inventory Optimization – Correctly Addressing All Factors,” at http://www.topdownleansystems.com/white.htm.
Dave McPhetrige
TopDown Lean Systems, LLC
Hi,
I had written a few weeks regarding SS calculations. I have taken a different approach to solving the problem (based on some research papers (one in Naval research logistics) I read):
1. Get Historical lead-time demand for a product
2. Perform Bootstrapping / Monte-carlo to replicate lead time demand
3. Get emperical CDF from bootstrapped replications
4. Derive re-order point for different “service levels”
5. Calculate SS by subtracting mean LTD from re-order point (as P(D <= meanLTD + SS) = CSL
I think approach is working ok. I had a question about the standard formula though:
1. Can we use historical demand variability (represented by standard deviation) if we don't want to use forecast error variability in std. safety stock calculations?
Verrami,
Using historical standard deviation is OK, but why don’t you want to use forecast error?
http://www.stuart.iit.edu/shared/shared_stuartfaculty/whitepapers/thomopoulos_safety-forecast.pdf
Ritu,
I suggest that you contact me through http://topdownleansystems.com/contact.php, so I can give you a thorough reply to your questions. On this blog that Larry Loucka so kindly provides, I’ll give an abbreviated answer.
You’re right, for components, the best source of usage is inventory transactions — backflushes, work-order issues or closings, scrap transactions and miscellaneous issues. (Be sure to exclude receipts, inventory-location moves, cycle counts and inventory adjustments.) Of course, your MRP system keeps track of the daily details for these transactions — date, part number, transaction type and quantity. I think the monthly-data problem that you’re running into may be because you’re using a “front-end” summary report. You may be able to get daily transaction data by using a “back-end” query on the MRP inventory-transaction data tables, and your IT group may be able to help you with this.
Also, you’re exactly right: 12, or even 24, data points do not provide a good sample size for statistical analysis. There is no magic that can provide reliable statistical results from inadequate data. If you can get daily usage data, you will have perhaps 250-360 data points in a year (even if some of those data points are zeroes), which is a much more reliable sample. Safety stock is all about quantifying common-cause random variations, and the only way to do this is by using as much historical data as you can get.
We have a white paper that discusses the many various safety-stock formulas, and how to determine correct safety-stock levels. Click on the “Service Level and Inventory Optimization – Correctly Addressing All Factors” link on http://topdownleansystems.com/white.htm.
Dave McPhetrige
TopDown Lean Systems, LLC
hey david,
Thank you so much for your views. Whatever you have written, I felt it is so so true. Infact I asked the buyer to give me max-min and average lead time estimates. Also we had a discussion on over safety and under safety in case of two bins just as you indicated. However, we are dong few permutations and combinations where we can work out optimal inventory value.
i have a question, as discussed with lawrence earlier, I have monthly consumption data as they do backflusing of stock on certain random intervals from mrp. hence i have (monthly-consumption)/(working days)=average daily demand. So in this case i suppose working out standard dev of consumption/demand for 12 data points will not be so accurate. And then, where i shud multiply the service level? I am confused here.
In such case which formula i can use for determining safety stock.
Thank you.
Regards
ritu
Steven,
We have a variety of white papers discussing optimal safety-stock levels, their resulting expected average inventory on-hand and other related inventory-velocity measurements, along with expected results for other key indicators involving reordering, demand and demand intermittency. I invite you to take a look at them at http://topdownleansystems.com/white.htm. Also, I’ll be happy to discuss safety stock with you. You can contact me at http://topdownleansystems.com/contact.php.
Dave McPhetrige
TopDown Lean Systems, LLC
Ritu,
Just a few more thoughts on safety stock for your fast-moving, high-consumption purchased components of your injection-molding machines:
Forgive me for asking what may be a dumb question, but is the lead time on at least some of these items short enough so that you can wait until you have the customer order before you have to order the required component? If so, then you don’t need safety stock (unless you incur scrap or yield).
Also, it sounds like you have significant seasonality, since your capacity is 95-100 per month and your demand is 120-140 per month. You must have a slow season during which you “get ahead,” right? If this seasonality is predictable, you may want to have a separate safety-stock level for each season, and you may need little or no safety stock for at least the low season.
On the topic of lead-time variability: As you pointed out, system data on historical actual lead times can be unreliable for a variety of reasons. In such as situation, what I often do to determine lead-time variability for a component is ask the buyer what he/she thinks is the average lead time. Then, I ask for the estimated “gut-feel” shortest lead time that occurs at least 2% of the time, excluding infrequent special causes such as natural disasters. Finally, I ask for the estimated “gut-feel” longest lead time that occurs at least 2% of the time, also excluding infrequent special causes. I then use these intuitive, experience-based estimates of lead time and variation.
You mentioned that the buyer would like to implement two-bin kanban for replenishing these components. As you know, this technique has the benefits of being 1) simple and 2) visual. Because it’s visual, it is not affected by the inventory-transaction/inventory-counting inaccuracies you mentioned (assuming that the MRP order policy isn’t automatically generating re-orders, and/or that the buyer is ignoring MRP’s re-order suggestions, and is using kanban signals instead). However, applying optimal safety stock to a two-bin system is not easy. For example, let’s say that you have used some sort of statistical model to determine safety stock, and that the calculated safety stock quantity is 100. If you add 100 to the quantity in each of the two bins, you have too much safety stock, slow-turning bins, poor inventory performance and a higher-than-desired service level. (Granted, if the value and carrying costs of the extra inventory are minimal, then from a practical perspective, it doesn’t hurt to carry a little extra inventory.) On the other hand, if you divide the 100 evenly, adding 50 to each of the two bins, you don’t have enough safety stock on hand, and so you won’t consistently achieve your target service level.
We have developed a safety-stock service that determines optimal safety-stock levels specifically for two-bin kanban. I’ll be happy to give you more details on it. Feel free to contact me at http://topdownleansystems.com/contact.php.
Dave McPhetrige
TopDown Lean Systems, LLC
hey Lawrence,
The time 3 months for m/c making is because from the time order gets punched and special specifications processed, it takes about a week or so and then after the parts attachments is done in system, the purchase gets requisitions. Also the rate of monthly orders is 120-140 and their capacity is 95-100 m/c per month and hence the capacities for next two months are nearly full. So the assembly start date is usually 2-2.5 months after the sales order is recieved. The time for assembly is generally 4-5 days, 7 days continuous testing and then the final touch ups and dispactch, all these makes about 15 days from assembly start date.
Onquestion of how they get requisitions is, the onhand balance gets assigned to the safety stock and open demand and shortages are given for the unfulfilled demand. They use lot-4-lot for most of the items, some of them also use periods of supply. My focus is just on fast moving, highly consumed items for which the buyer is trying to implement twobin supplier kanban, hence the safety stock determination.
The PO history as u suggested can be got but buyer is apprehensive to rely on it because many a times the supplies are deferred and worked out on scheduled m/c start date so it may not reflect the true picture of supplier lead times. However i have also requested for the past daily usage data.
Thanks for your reply
ritu
I just realised that the back testing approach described above is actually just shifting the past average stock level downwards. This approach seems however not to work in my case. I can shift the lowest past stock level to zero, but because this lowest level is determined by an exceptional event (problems with receipt) and is close to zero, the stock reduction will be very small. Because I am told by my boss to not take into account the exceptional events, I thought about determining a virtual SS line, described above, to filter out these exceptions. This seems however not to be a scientific approach to determine what stock reduction could have been possible.
Therefore, I also thought about determining, in addition to the safety stock level, an equivalent saw tooth stock profile for the past data, but I am not sure that this would give the correct average stock level. I would calculate the equivalent lot size (or inbound batch for the inbound buffer) by dividing the total yearly demand by the amount of setup times used(or amount of deliveries for the inbound buffer). Dividing this by 2 would give the cycle stock and adding up the SS would give me the average stock that could have been in place if my safety stock would have been taken into account. What do you think about this approach, could it deliver a useful “new” average stock levels which can be compared with the past average stock level?
Thank you in advance for your opinion about these thoughts!
Steven, with back testing you should use you new safety stock levels to trigger the replenishment. Pick a reasonable starting inventory level as an assumption. You subtract the actual consumption from the prior period (day?) stock on hand and you add the supply based on what could have happened if the new rules were in place back at the beginning of the model period. Keep in mind that if you never stock out (run inventory to zero), then you are carrying too much safety stock. To never stock out, not once, you would have to have almost infinite inventory.
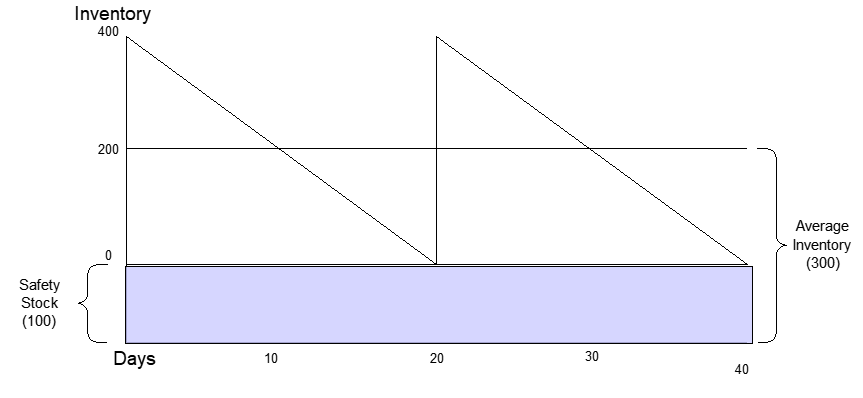
Yes, the area under the ‘saw tooth’ is your expected or average inventory. A simple formula is, average inventory = (0.5 * (demand * lead time)) + safety stock.
Hi Lawrence,
TY for your answer. The first production plant has several customers, including the second plant. Therefore, both outbound of the first plant and inbound buffer of the second plant have to be determined.
Let me explain the situation more in detail. The plants do not have a theoretical approach concerning stock management and therefore no safety stock methodology as such is applied. However, they currently do have excess inventory (so they do have safety stock, but this is fluctuating during the year, without reason). One of the goals of the project is to calculate the necessary SS level in order to reduce these excess inventories and to bring some regulations regarding reorder point etc.
So if I understand you correctly, to apply back testing, I have to start from my calculated safety stock level and add the actual past receipts and substract the actual past demand in order to have the stock level that they could have had?
A second approach I thought of was determining a “virtual SS line” (for instance the level where 90% of the days, the actual past stock is above this line). But probably back testing is more correct approach :).
Dear Lawrence,
I am a MBA student doing my ineternship in plastic injection molding machines manufacturing co.. The Co. has fixed customer orders for next 3 months and some buffer machines planned so as to generate requisitions for long lead parts. eventhough the demand is known many a times they run on excess stock and many times understock due to issues of stock discrepancy.
Being in purchase department I am trying to work on safety stock of certain fast moving items for a buyer. The data available are: Past monthly consumption, past monthly demand data in cumulative terms, last year total consumption. The leadtime is in days.
Hence i am confused as to how i should get the actual daily consumption data in order to calculate the accurate SS figures as explained in earlier posts. As the demand variability is also huge because the machines are made as per customers specs and very few items are standard. Moreover min or max LT is very vague as the track of actual leadtimes is not there. I have LT figure that is defined in the system (Oracle JDE E1-ERP).
I request you to suggest me, which formula i can use, which data to consider for avg demand and what should be my approach to detremine the lead times for accurate calculations of safety stock.
Regards,
ritu
If you can’t get demand by day then you can convert your lead times from days to decimal months. 10 day lead time is half a working month.
But when the top level item is custom and there are very few common parts between model you may need to move safety stock closer to the suppliers. Maybe you don’t know exactly which parts your will need but you might know what bar stock the supplier will likely use.
“Standard” Lead Times in the system are always suspect. You should test this by looking at some of the PO history: PO create date, item request date, actual receipt date.
Are component (purchased parts) requisitioned out of stock and issued to the finished product work order? If so, then there should be transactions and paperwork. But calculating average daily demand may not be appropriate for your business if the ordering, production, shipping, and billing are on a monthly cycle. Shifting gears and getting your business to run at a higher velocity is a whole different issue. Why does it take 3 months to build an injection molding machine?
Dear Lawrence,
I am currently doing a SC project where I have to design the optimal stock level for both inbound and outbound buffers of two production plants.
Therefore I used the well-known safetystock equation {Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}.
However, these production plants did not use any safety stock methodology in the past (I have past stock data per day where this is visible). My question is now how to define the stock reduction (and related the working capital improvements) resulting from my safety stock calculations. (Note that I only can work with past data, because forecasts are currently unreliable).
My guess was to calculate the average stock that would have been in place if my safety stocks would have been applied and compare this with the past average stock level (which is given). If this methodology is correct, could you give me some more insights about how to do this. If not, how would you tackle this?
Kind regards,
Steven
Steve, why both inbound and outbound buffers? Why not only one buffer? If the two plants operated without safety stock in the past why are you adding safety stock now? Sometime we add safety stock as a way to reduce work-in-process. i.e. get all the excess stock off the shop floor and put it where we can see it and control it. Sometimes we add safety stock because our replenishment lead times are too long, longer than the customer or market wants to wait. What are you trying to do with your safety stock, and are there no other ways besides adding stock?
I like your idea of calculating inventory levels if you had been using new rules in the past. We call this ‘back testing’ – use the actual demand that occurred and calculate daily on hand inventory by taking a starting inventory level and adding receipts and subtracting consumption. Then you can compare the actual inventory levels vs your new model.
Rafal, Suggest you research Multi-Echelon Inventory Management. Keeping stock at multiple locations isn’t ideal. Long lead time is also a complicating factor. You can calculate safety stock for each location independently. Can stock or customer orders easily move between the several forward locations? If not then you may not want to “pool” the safety stock. Lawrence
Dear Lawrence,
Do you have a formula that can calculate safety stock for both together: manufacturer and buyer? I am working on a stock policy for some materials that are produced in one factory and sent to several others within the same company and I would like to define total safety stock that should be kept on noth sides. The forecasting between customers and manufacturer is in place and we measure its accurancy, so if the formula was taking forecast accurancy into account, it would be great.
Lead time is quite long (60-120 days) and safety stock is used to cope with extra demand (which is standard).
Thank you in advance for your help.
All the best
Rafal WIsniowski
Verrami,
In reply to your first question about lead time < 1 month: Analyzing demand variability using monthly historical data has two drawbacks. First, it allows demand peaks and valleys to offset each other, lessening their true impact. Second, it reduces reliability, since each year of historical data provides only 12 data points. Daily data is the best.
I’m sorry, but I don’t understand your second question about safety stock < average demand. The safety stock needed to achieve your target service level consistently and with minimal expediting may be relatively small or relatively large, depending on the combined effects of six key factors that drive safety stock.
The simple safety-stock calculation you’re asking about considers only one (demand variability) of the six factors that affect safety stock, service level, inventory optimization and expediting. We have a white paper, “Service Level and Inventory Optimization – Correctly Addressing All Factors,” that discusses how to establish safety stock that consistently achieves your service-level targets with the minimum safety stock possible. I’ll be happy to send you this white paper. Feel free to contact me at http://topdownleansystems.com/contact.php.
David McPhetrige, TopDown Lean Systems
Thanks for the clarification. I had the same issue with adjusting the stdev like that but given that Var(aY) = a^2*Var*(Y) and approximating Var (Month) = Var (30*Day), I thought I could do it. Also, I read on some websites online where they convert a daily stdev to monthly stdev using that approximation.
The first question I had was whether the SS makes sense, from a definition perspective, if LT < Month. Does it still provide SS value to prevent stock out during lead time? Also, If SS is < Average Demand, then how feasible is it to provide that coverage?
I had a question about the basic SS formula (considering only demand variability). The event based SS = z*sqrt(L)*Stdev(Demand).
I have demand at a monthly level but my lead times for parts is < month (for e.g., 15 days). For now,I have transformed lead time in days to a monthly level and calculated the SS. My question is whether this translation and subsequent calculation is accurate or not?
For e.g., lead time is 0.5 months, StDev (Demand, Month) is 500 units, so
SS = z* sqrt(0.5)* StDev(Demand, Month).
Basically, I am struggling with the interpretation as the formula provides SS value to prevent stock outs over lead time. If I do the transformation, then should does the interpretation still stay the same?
Also, If I do need to calculate SS over lead-time, then would this derivation of stdev and SS work:
Stdev(Demand, Day) = StDev(Demand, Month)/Sqrt(30)
Stdev(Demand, LT) = sqrt(LT)* StDev (Demand, Day)
SS = z*sqrt(LT)*StDev(Demand, LT) = z*sqrt(LT)*Sqrt(LT)*StDev(Demand, Month)/Sqrt(30)
Thanks!
Sorry, but you can’t ‘adjust’ standard deviation like this.
Using z = 1.64, then SS = z * sqrt(0.5) * 500 = 355
Eva,
A few more thoughts on your van service parts: First, as Larry points out, if you can lengthen the customer lead time, you can avoid many of the safety-stock challenges of low-volume, intermittent-demand inventory items.
Second, for really low-volume items, where you never use more than 1 or 2 during the van replenishment lead time, the van should carry 1 or 2 of these items. Forgive me, I know this is obvious, but I’m pointing it out because it may narrow the number of inventory items that need a more elaborate safety-stock analysis.
Do your customers demand high service levels? Do they expect those service levels (with no backorders) directly from the vans? Is expediting van shortages from the vans’ supply point cost-prohibitive for you? If so, and if your van-inventory items are low-volume, intermittent-demand (a lot of days with demand = zero, and a right-skewed distribution for demand > 0), then a simple safety-stock calculation will put either too much or too little inventory in the vans.
I’ll be happy to help you with safety stock that will give you the right balance of inventory and service levels. Please feel free to contact me at http://topdownleansystems.com/contact.php.
Dave McPhetrige, TopDown Lean Systems
Eva, High Variability parts (where Cv=STDDEV/AVERAGE > 1.0) are always tricky. You either carry too many or never have enough. Vans, unlike warehouses, can carry only a very limited number and quantity of parts. High Cv parts are often better handled as special order or with longer leadtime. (I’ll give you some today and the rest the next time I come to town.)
How long does it take for the van driver to decide parts are needed, place an order, and get the parts? Safety Stock could simply be cycle stock (average daily demand * reorder time) + (stddev * z).
Lawrence
Hi Lawrence,
I was thinking of using the formula: {Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}, but I wanted a way of accounting for those parts that have high variability in usage per job.
~90% of the parts are shipped directly to and are stored on the vans, only fragile and high-end parts are kept at the sales centers (mini-warehouses). I am in the processing of reviewing demand history to figure out what to keep on the van, and I need to figure out the SS levels for them.
Thanks.
Eva.
Hi,
I am thinking of using this formula for determining the safety stock levels for parts in a set of service vans, are there any other factors that I need to consider? I was thinking of accounting for the intermittence of the demand by choosing the max of the StDv and a factor of the average demand… Any advice would be appreciated.
Thanks.
Eva
Hello Eva, Service Vans are just small warehouses on wheels. Assuming your vans have a defined territory then like a warehouse you can review demand history and do some analysis to help decide what parts to stock and how much. Do you vans come back to a master warehouse every day, or do you ship parts to the van whenever the van driver makes a parts order? Do you know how many of each part are on the van at all times? Once a day? Once a week? Or only the driver knows?
Which formula are you thinking of using?
Lawrence
Good morning,
I have ordered the book on forecasting for dummies but in the meantime it arrives,
i went on internet to try to see how it works and i have a few questions.
Moving average: in one site they had that example with column 1 going from jan to december showing the actual sales and in column 2 was the moving average forecast. in that example they were taking the average of 3 months. on one site the guy was entering the formula (average of jan, feb and march)in the april cell of column 2. In another site the guy was entering the same formula in the cell of march in column 2. Which way is correct? and then a very ignorant question sorry but the result,does it constitute your forecast for the following year (surely it can’t be?) or just the forecast for april of the same year, but in which case how do you forecast the following year?
Taking seasonality into account when doing an exponential forecast and also growth if there is growth between years. i have done a wee excel example and was wondering if one of you could have a look and advise if i am in the right direction?
thank you, kind regards
maite
Hello Maite, Sorry for my slow reply. I am in Belize and the internet here is up and down.
Moving average forecast is not always 3 month average. You can take any number of historical periods. The average of the last 3 months is a common forecast for next month.
Moving average is usually used to predict the next forecast period.
Moving average can be used to forecast other periods such as Next August based on the average of the last X August’s.
Weighted Moving Average gives more weight to the most recent period.
Send me your wee little spread sheet and I’ll look it over.
Why do you need to forecast next year? Do you have long lead time items that you need to buy now for next year?
Suggest you think about growth, and seasonality separately
For seasonality I like having 3 or more years of history. Then calculate the monthly (or weekly) grand average. Next calculate the average for each month or week – average of the same month (or week for the past X years). Now for each month (or week) calculate % above or below the grand average. This is now your seasonality factor.
Calculate or estimate or guess at your growth rate and apply the growth and seasonality factors to each period.
Look here … http://home.ubalt.edu/ntsbarsh/stat-data/forecast.htm
Lawrence
John,
Yes, I’ve had the same experience – subjectively-developed forecasts tend to be biased high. Let me start with a caveat: If the forecast is consistently biased, the best option is to quantify the magnitude and direction of the bias, and then correct the forecast for bias before authorizing it. Easier said than done, of course, but if the forecast is both generated and executed internally, this is a fundamental step that is critical to meaningful S&OP.
Having said this, I know that often a forecast is generated by one company, but it is executed by a third-party supplier or contract manufacturer. In this case, the third party may have little or no part in the customer’s S&OP meeting. If this is your situation, then you may need to correct the forecast bias yourself.
You’re right, if you buy (or make) an inventory item to a biased forecast, you can compensate for the bias by adjusting safety stock by the bias, if:
1) The forecast for the inventory item has positive bias that is less than or equal to safety stock and its current fill-rate performance is excessively high, or
2) The forecast for the inventory item has negative bias, currently requires safety stock and its current fill-rate performance is excessively low.
If your safety stock is properly modeled, and you haven’t adjusted for bias, your actual fill rates should be higher than desired for items with high bias, and lower than desired for items with low bias. This presumes that safety stock has been correctly calculated from daily fulfilled-demand values. If you have already adjusted safety stock for bias, and you still aren’t achieving your target fill rates, then your safety stock is not properly modeled.
Buying/making to a biased forecast may not be your only option. You may be able to use the forecast, bias and all, only for identifying exceptions. Obviously, the purpose of a forecast is to foresee the timing and magnitude of trend, seasonality and predictable special causes. The purpose of safety stock is insurance against the unpredictable timing of common-cause random variation. Properly-modeled safety stock, using historical actual fulfilled demand that is untainted by bias (and other forecast flaws), will tolerate a surprising degree of trend and/or seasonality. If your trend/seasonality is not dramatic, and if you update your properly-modeled safety-stock levels perhaps four to six times per year for trend, or once per season for seasonality, you may be able to use actual-history-based ROP (with proper safety stock) instead of forecast-based MRP for replenishment. This would disconnect your operations from the unavoidable inaccuracies of the forecast and enable you to replenish based on fulfilled demand. Of course, you would still have to watch the forecast for predictable special causes that may require one-time incremental buys (or makes), and for significant changes in trend/seasonality. In my experience, the combination of ROP and forecast exceptions can be more effective than replenishing to an unrealistic forecast.
In your post, you referenced the various safety stock formulas at the top of this blog page. All of them have weaknesses that prevent them from reliably providing consistent service-level achievement, optimal inventory performance and minimal expediting. We have white papers on this topic at http://topdownleansystems.com/white.htm, and a new one available through Supply Chain Digest at http://www.scdigest.com/login.php?cid=4349&ctype=content).
Dave McPhetrige, TopDown Lean Systems
Thank you very much for all the above, I will follow the advise of back testing and buy these books:- )
To come back to your first point indeed here the policy is to make to order.Forecast drives mainly the purchase of dry goods that we bought 1 month in advance for some, 3 months in advance for some others and 6 months in advance for the expensive ones. Forecast drives production(bottling as we bottle whisky here) only for our consignement warehouses and for some customers who can not afford to give their orders in our lead time (our lead time is 28 days most of time. All the rest is make to order only. They also use forecast to plan capacity at a high level and whisky avaibility on a long term view.The best level of forecasting therefore(excluding consignment warehouses stock)could be at pack level (for example by pack I mean our case of 6 bottles of 70cl)as labels are not an issue as they are purchased in very large batches and not forecast at SKU and customer level as they do here at present. But this level does not exist in the BOM at present. As the company moves to a new system next year,re-visiting the bill of materials has been recommended to them. Also the company grows and last year they ended up in trouble in October as there was a huge peak in demand and production fell behind. so they will rely on forecast more and more as they continue to grow and this year they plan to produce in advance for year end. Forecasting is all in excell at the moment and there is no model set up.
Kind regards
maite
Maite, you could let others handle the forecast details for you. One example is http://www.lokad.com/
where you upload your data and they give you back a best fit forecast.
Dave,
In my experience most forecasts, if not prepared using some statistical methods, are biased high. Over forecasting means purchased part quantities (dependenet demand)are higher than they need to be to meet actual demand. Assuming parts are bought in quantities matching the forecast shouldn’t average forecast error be added/substracted from any of the above standard (risky, wrong) SS formulae to eliminate the affect of forecast bias.
Regards,
John
Good afternoon,
I have a question regarding best method for forecasting.
First about the methods, I have found these ones on internet:
single average
moving average
weighted moving average
moving average with linear trend
single exponential smoothing
single exponential smoothing with trend
double exponentialsmoothing
double exponential smoothing with trend
adaptive exponential smoothing
linear regression
And my questions are: – Are there other ones? – where can i find a good explanation of what they entail doing? (I find some explanation on the web but it is so unclear or the way the calculations are explained is so technical that it is unclear to me).
2/ when you have one product, and history and you need to forecast, what would be the methodology to determine the best forecast calculation/method to apply to this particular product?
Thank you very much,
kind regards M.
Maite,
The best forecast is no forecast. Why cant you make-to-order (MTO)? Assuming your customer does not want to wait then you may need to make-to-stock (MTS). Suggest you look into “late stage differentiation” to help decide at what level of the Bill Of Material is the right level to MTS.
One approach for selecting the ‘right’ forecast method is called “back testing”, or Focus Forecasting. Go back in time a year or so. With the history you have calculate new forecasts using every equation. Then compare the forecasts to the actual results for that time period a year ago. Then come forward one period and calculate and compare again, and again, and again. For each forecast method calculate the forecast error – Mean Absolute Percent Error (MAPE) and Mean Absolute Deviation (MAD). Then use the forecast method with the lowest error for your real future forecast.
Forecasting and time series analysis are very deep subjects. People get PhD’s in this. Suggest you pick up an forecasting introduction book. Try Forecasting for Dummies by Conrad George Carlberg, or Focus Forecasting by Bernard Smith.
Good luck!
superb, thanks very much for all of the above,
kind regards
CoudeM,
Usually, inventory-carrying costs involve:
.Cost of money
.Taxes
.Insurance
.Warehouse expenses
.Physical handling
.Inventory control
.Obsolescence
.Deterioration, damage, pilferage
You will find many textbooks that address carrying costs. Typically, they suggest a total inventory-carrying cost of 25%-55%. It’s important to use a carrying-cost estimate that your company buys into.
In my experience, the lost sales resulting from too little stock are best estimated by your marketing/sales organization. You’ll need to use a financial model to analyze the financial impacts. Remember, as you lose sales, and therefore volume, you de-leverage all of your fixed costs and expenses. In addition to lost sales volume, you may also experience reduced pricing as your service levels drop, since your customers may perceive less value in buying from you. Finally, as stock levels and service levels drop, your expediting costs may increase significantly.
I invite you to check out our white papers on safety stock, inventory optimization and customer-service levels, at http://topdownleansystems.com/white.htm.
David McPhetrige, TopDown Lean Systems
sorry meant to post Thank you very much in English:- ), I find the documents sent very useful.
one last question: what data would I need to calculate:
-risk of holding too much stock ? does it have to be in terms of profitability for the company?
or would it just be cost of space, cost of items (manufacturing cost)?
-risk of not holding enough/loss of revenue? this one would be profitability in terms of sales?
-Is there a best business practise methods/calculations to identify these risks?
KInd regards
oh merci! j’envoie l’example dans l’email, merci tellement:-)
Hello,
I am in a desperate need for help. i am junior in planning and trying to work out safety stock. My company has given me a dead line for tomorrow but
I must misunderstand what the formula really means {Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2} as the result it gives me I don’t understand. Could I please check with you?
I am working from a warehouse model, therefore where i have depletion forecast, actual,reorder to replenish the stock and safety stock.
{Z is the service level factor this is ok
Avg. Lead Time is the transit lead time to get the goods correct?
Standard Deviation of Demand: it is of the past demand yes? should I exclude christmas when I have seasonality?
Avg. Demand: what is this? is it based on past demand or future demand?
Standard Deviation of Lead Time: this ok, I see what it is.
what do you do when you ahve a market where the depletion forecast is always false? could you put a average all over the forecast and work with safety stock to absorb the fluctuations should the demand reach its highest point of lowest point?
–then the reorder point, should it be just lead time demand +safety stock?
-Lastly, what about the quantity to re-order? is it just the forecasted demand during lead time but from the point at which your stock is received? when you determine what quantity to order, can you take into account any correction that would have been made in between times to the “actuals”.
I have build a small model and wonder if anybody would mind looking at it to give me an example based on my data on how to calculate the safety stock?
sorry for the rush, I really hope one of you can help me, many thanks!
M
M
Average Lead Time is more than Transit Time and can include supplier order processing time, manufacturing lead time, order picking and packing time as well as your receiving time.
Standard Deviation can exclude outliers and abnormal demand periods. With seasonality we will often include seasonality adjustments the safety stock.
Average Demand is often historical, but that is like driving a car by looking in the rear view mirror. So We usually us history to calculate standard deviation and forecast to calculate average demand.
Forecasts are always wrong, some are useful. Can you measure the forecast error? Is it better to have too much safety stock or too little? Not a trick question. What is the cost of too much? What is the cost (and lost revenue) of too little stock? For an unpredictable market consider ways to reduce lead time and shift from Make (or Purchase) to Stock, to Make To Order.
Reorder Point is Average Demand * (Lead Time + Safety Time).
Reorder Quantity can fixed quantity, fixed period, or reorder up to Max. Suggest you look into the topic of Economic Order Quantity.
Send me your model info@resourcesystemsconsulting.com
Rohit,
I have the same questions as Larry outlined. And I’d like to add four more questions, please:
1) What safety-stock calculation or technique are you currently using?
2) Are you trying to determine safety stock at the retail outlets for your FMCGs, or at a distribution center?
3) Do these products have a restrictive shelf life?
4) When customer demand cannot be fulfilled on-time, is it canceled, or does it become past-due backlog?
Your observation is spot-on: Std dev is only one part of optimizing inventory / financial performance and consistently achieving your service-level targets. When you use it as the sole definition of demand variability, you are likely to come up with excessively-high inventory levels, and this is even worse if you use an event-based z-value safety-stock calculation.
Your statistical analysis of demand distribution must also identify skewness, since demand is rarely normally-distributed. Seasonality may require multiple, season-specific safety-stock levels; or else a statistically-sound approach to de-seasonalizing your demand data. Also, as you pointed out, marketing schemes (if those are the “schemes” you referred to) are special causes, and you need to exclude their impact from the random demand variation you’re trying to isolate with std dev. In other words, your safety stock needs to exclude variation for which you can forecast both timing and magnitude: seasons, trends, schemes, etc.
Demand variation is not the only factor that affects safety stock, fill rate and inventory optimization. Other factors include lead time, lead-time variation, replenishment interval, minimum order quantities, order multiples, lost sales, demand intermittency and the quantity-based (not event-based) way you measure service level. We have many white papers on these topics. I invite you to see them at http://topdownleansystems.com/white.htm. Also, please feel free to contact me at http://topdownleansystems.com/contact.php.
hi..i just wanted to know how to calculate the standard deviation for an fmcg company while calculating safety stock
As for an FMCG company the demand for each month is dominated by the schmes.So in this case if we simply calculate the std deviation . I guess we land up getting high safety stock and high inventory
Rohit Lohani
Rohit Lohani, do you ship only once per month? You say demand for each month is dominated by the schemes. Please explain. Demand isn’t the total of all orders for the month. Demand is the quantity that you need to ship on each shipment. Maybe you should be calculating the average daily demand and standard deviation.
Larry Loucka
Dear Lawrence and dear David,
thanks a lot for your help and advices. I will observe proposed methods how will be aplicable in my analyses.
If need more clarification I will come back to you
regards,
Tanya,
We have two white papers that discuss the formula Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2). They are “Common Safety Stock Calculations” and “Safety Stock Formula Involving Lead Time Variation.”
We also have another white paper, “SAP Safety Stock Formulas Derivation,” that goes into detail on safety-stock formulas that utilize forecast error. You’ll find these white papers, and others related to safety stock, at http://topdownleansystems.com/white.htm.
Abhishek,
We have several white papers discussing a correct way to determine safety stock when demand is right-skewed and/or sporadic. I invite you to take a look at them at http://topdownleansystems.com/white.htm. Your concern is valid. Most demand distributions are right-skewed because the lower bound is zero while large demands have no limit. Also, a high percentage of inventory items experience at least some degree of sporadic demand.
Lawrence makes an excellent point on the make-to-order option. Safety stock can be expensive, especially for items with highly-variable and sporadic demand, and it’s part of the total cost of make-to-stock inventory ownership.
Tanya, yes the best way is to do the math with unit of quantity. You can do the math with unit of time, but this is not common and sometimes not easy to do. Customer Demand and Supplier Fill can vary both in quantity and in lead time. If I have Customer Order, Purchase Order, or Production Order history I always have a quantity and a date. Sometimes the quantity has problems. Maybe the quantity isn’t what the customer wanted, but is only what was sold. You need to “interview” the data. With dates it often gets even uglier. We need to calculate lead time, the number of days from the order to shipment, or order to receipt, or expression of desire to fulfillment. What dates to use – order entry date, quote date, planned ship date, request date, actual ship date,actual receipt date, etc. Then you should calculate the average and standard deviation of the number of days. You may want extra inventory to cover customers that want/demand very short lead time – “ship today or I will take my business to someone else”.
When you work with unit of quantity (or Kg, or Liters, or cases, etc) and not time you can use the formula you mention.
^ means to raise to the power of. ^2 means to square, or raise to the power of 2.
Here is my “simple” formula to set Min/Max:
AD = average daily demand
RT = replenishment time
SF = safety factor (or Z)
SD = demand standard deviation
Min = AD * RT
Max = (AD * RT) + (SF * SD)
Average Inventory = Min + 0.5(SF * SD)
Dear Lawrence,
Thanks a lot for your so promt answer. May we continue on this topic, if you don’t mind?
Just to be sure I’ve got properly your answer ( my english is not perfect and that’s why I’m not sure I’ve understood correctly your point) – you mean that the most correct way is to calculate safety stock in quantity and after that if need to transfer this number into days coverage ( based on expected demand e.g.) – is it?
If yes, and if you recommend this formula : {Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}.
Could you clarify what is this sign “^” – does it mean to be raised to the second power?
In fact I have to establish Raws&Packs Policy ( in the company) and need to prove how to be decided min stock levels ( and formula I found is min. stock = K + (k*fe*SQRT(LT), where:
K- safety factor in days ( I assume this is safety stock in days, don’t you think?; k= factor linked to the desired CSL ( in your formula called “z”); fe – forecast error; LT lead time.
So I have all other components and only don’t have K ( safety factor). That’s why I was wondering is there some easy way to reach it directly in days, but it seems not. What was my conclusion, reading your answer is that in fact I have to calculate safety stock in quantity per article ( or group of articles) and after that to calculate for how many days this safety stock makes coverage…
Do you think it is correct ( my understanding)?
Dear Lawrence,
I have following question:
What you could advice me in order to calculate Safety stock in days. I mean not to calculate safety stock in tons per articles, but somehow to choose for how many days/ weeks to keep “reasonable” safety stock. Do you think it’s correct and is it some way to calculate this safety stock coverage in days based on:
Lead time; CSL factor; what else…?
Thank you
regards,
Tanya
Tanya, good thinking! Yes, you can work with Safety Time. Maybe you want to keep some number of days worth of stock, but you know that demand can change from day to day, so you want to add some safety time. Usually we have a safety stock policy that can be something like “X days of average daily demand + Y days of safety stock”. Then for each part number you calculate the quantity that matches the number of days. Make sense?
How many days of safety stock? Well shat do you now about the demand variation during the X days? Can you calculate the demand standard deviation?
If demand is typically right-skewed, or sporadic, then what formula should be used for calculating safety-stock levels?
Maybe the right answer is zero; make-to-order.
David,
Thank you for your detailed response to my questions. This is very helpful information. The specific exmaple I mentioned has changed, so I will write back if any more follow-up is needed. In the meantime, I will check-out the white paper(s) you listed above for furter insight.
Again, thanks for your time and response.
Dan F.
Dan F,
We have the statistical derivation of the formula in your first point in a new white paper, “Safety Stock Involving Lead Time Variation,” which is now available on http://topdownleansystems.com/white.htm.
I’ll try to provide an intuitive explanation of why Avg. Lead Time is not squared. The formula in your first point asserts that the variance of total demand over lead time is:
Variance(Total Demand) = Avg. Lead Time*Standard Deviation of Demand^2 + Avg. Demand^2*Standard Deviation of Lead Time^2
Let’s use an example where lead time is given in days, and where the daily demand is normal with mean 50 and standard deviation 5. We will assume that lead time can be one, two, or three days, with probabilities .25, .50, and .25, respectively. Then the total demand over lead time is a mixture of three distributions, depending on the number of lead-time days, where these are represented in the proportions .25, .50, and .25:
One day: Normal, mean 50, standard deviation Sqrt(1)*5
Two days: Normal, mean 100, standard deviation Sqrt(2)*5
Three days: Normal, mean 150, standard deviation Sqrt(3)*5
The fact that the standard deviation of Total Demand, say, for a two-day lead time is Sqrt(2)*5 follows from rules for summing variances of independent quantities: the variance of a sum is the sum of the variances.
We will address the second term in the Variance(Total Demand) formula, Avg. Demand^2*Standard Deviation of Lead Time^2 first, and then will address the first term.
This second term describes the variation in lead times, but converts this to days. The variance in lead times is simply Standard Deviation of Lead Time^2. But Total Demand is given in items of demand, and so this quantity has to be converted to demand. To give a heuristic idea of what is going on: We convert lead times to their associated average demand values, so that we are looking at Avg. Demand*Lead Time. The variance of Avg. Demand*Lead Time is Avg. Demand^2 * Variance of Lead Time = Avg. Demand^2 * Standard Deviation of Lead Time^2. This is, intuitively, how the term Avg. Demand^2*Standard Deviation of Lead Time^2 appears in the formula.
The first term appears in the formula for Variance(Total Demand) because there is more to the variation of Total Demand than the variation in average demand at the various lead-time values; the variation of the demand distributions involved in the mixture must also be factored in. This is the role of that first term, namely, Avg. Lead Time*Standard Deviation of Demand^2.
In terms of our example, here is an intuitive view of how that term appears. The variance of daily demand, in our example, is 5^2. However, the distributions in the Total Demand mixture have different standard deviations depending on the numbers of lead-time days. As we saw, the standard deviations for these component distributions are given by Sqrt(k)*5, where k = number of lead-time days. When squared, these give the variances k*(5^2). The first term in the formula takes the average of the individual lead times and multiplies this average by the variance of daily demand, in our, example, Avg.Lead Time*Standard Deviation of Demand^2 =2*5^2 = 2*25 = 50.
The short answer to your second question is: Establishing safety stock for each demand stream, and adding together the results of each, would be a safe, conservative approach. We use a technique that is more complex, but that also finds a more optimal balance of inventory levels and service-level performance.
I have some additional questions that could help provide a more clear answer to your second question:
1. What criteria determine the sourcing for any given demand for Raw Material X? In other words, the distribution shape and scale of these two demand streams may be significantly different, even though the overall demand split is 50-50. The formula you have cited assumes, among other things, that demand is normally distributed. Likely, X’s demand is right-skewed, and perhaps even sporadic.
2. What are the lead times for each sourcing scenario? You have stated the replenishment intervals (every 7 days, every 30 days), but you have not indicated the lead times. On this topic, notice that the formula you cited does not have a term for replenishment interval, even though replenishment interval can significantly affect safety-stock requirements. As you know, lead time and replenishment interval are not the same thing, and it’s simply coincidence if the two are equal.
3. When you say 95% service level, do you mean a quantity-based fill rate, or an event-based probability of no stockouts? Your cited formula is event-based. My guess is that when you measure your actual service-level performance, you use a quantity-based fill rate. These two service-level criteria are not the same, and the difference can be substantial.
In addition to the white paper I mentioned above, we have three other white papers on the topic of safety stock at http://topdownleansystems.com/white.htm. Also, we’ll be happy to discuss safety-stock details and specifics, so feel free to contact us at http://topdownleansystems.com/contact.php.
David McPhetrige, TopDown Lean Systems
Hello,
I had two questions I was hoping you could look at and respond….
1) Formula question: Why is the Average Lead Time term not squared in the equation? Can you explain this in “layman’s” language, maybe with an example?
{Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}
2) Plant A uses Raw Material X (10 units day +/- 3 units). Raw material X is stored in Warehouse 1. Raw Material X is shipped by truck from Warehouse 1 every Friday to Plant A (1 day +/- 0.5 days). Raw Material X is sourced in Warehouse 1 at 50% by local supplier (truck arrives every 7 days +/- day) and 50% by import supplier(ship arrives every 30 days +/- 7 days). What would you recommend to calcualte the “total” system safety stock for Plant A to insure 95% service level and why? Do you make two calculations and add them together(i.e. one for local and one for imports)? Any help would be great.
I’d apprecaite your feedback and advice.
Thanks!
Allan,
Short answer: Let’s address the first formula that you cited in your post, which we will call Formula (1) in what follows:
z * SQRT(avg lead time * std dev demand^2 + avg demand^2 * std dev lead time^2).
This formula is stated correctly, given the event-based service-level criterion that it intends to optimize (and with the understanding that the expressions involved are the means and standard deviations of the relevant theoretical distributions).
Expanded answer: Formula (1) is based on the distribution of total demand over lead time, where lead time is allowed to vary according to some probability distribution. It can be shown that the standard deviation of the total demand over lead time is precisely the square root given by the formula, namely, SQRT(avg lead time * std dev demand^2 + avg demand^2 * std dev lead time^2). We are currently preparing a white paper that discusses the derivation and shortcomings of this formula; this paper should appear on our Website shortly. If you (or anyone else) would like a copy, please contact me at http://topdownleansystems.com/contact.php.
Before discussing the other two formulas that you mentioned, we need to say that Formula (1) can give extremely misleading results. This formula’s computed safety-stock values can be excessively overstated (poor inventory velocity) or inadequate (poor actual service levels). These values are highly sensitive to the distribution of lead time. This is illustrated in the white paper that we are currently preparing. Again, if you are interested, please contact me for a copy.
Concerning the second formula that you listed:
z * SQRT(avg lead time^2 * std dev demand^2 + avg demand^2 * std dev lead time^2 + std dev demand^2 * std dev lead time^2).
We are not familiar with this formula. The square-root portion of this formula cannot represent the std dev of total demand over lead time, since, as mentioned above, the square root in Formula (1) is the correct expression for this. Might this be a std dev for a different situation? Could you provide an explanation of how this formula is derived, or where you might have seen it published? We are very interested in its source.
Concerning the MAD-based formula that you listed: In this formula, the std dev of demand in your second formula has been replaced by MAD. As you know, the use of MAD implies that demand is being forecast. So, whereas Formula (1) is built around actual demand values, using MAD in a safety-stock formula presumes that safety stock will be computed to guard against forecast error. Although it is true that MAD can be used to estimate the theoretical std dev of forecast error, it is a flawed approach that is inferior to simply using the sample std dev of forecast errors as an estimate of the theoretical std dev. However, whenever MAD is used to estimate the std dev of forecast error, it must be multiplied by a factor of approximately 1.25; in other words, the theoretical std dev of forecast errors is estimated by 1.25 * MAD.
Using forecast-error MAD to estimate the theoretical std dev of forecast error is suboptimal. The sample std dev of forecast errors gives a better estimate of the theoretical std dev of forecast errors than does MAD. Using MAD made sense when computing power was minimal, but today the use of MAD to estimate a std dev is not defensible.
Additionally, using MAD to estimate the theoretical std dev of forecast errors can be problematic for a number of reasons:
1. The typical use of MAD to estimate the theoretical std dev of forecast error requires that forecast errors be normally distributed with mean zero. However, actual demand values are often right-skewed, and sometimes highly so, especially in cases of sporadic demand, leading to non-normal forecast errors.
2. Forecasts are biased for various reasons, especially at the inventory-item level. For example, an inventory item’s forecast demand may be chronically under or over actual demand. In such cases, forecast errors will not have mean zero, making the computed safety stock-value suspect; this could lead to safety-stock levels that are much too high, or dangerously low.
3. Many common MAD-based safety-stock formulas also assume that the forecast errors are independent. Often, forecasts are based on demand values from previous periods. Although this does not necessarily mean that the errors will fail to be independent, in many cases, the errors could fail the independence requirement, again making the computed safety-stock value suspect.
4. The time frame of typical forecast periods decreases the number of forecast-to-actual deviation data points. For example, if the forecast period is one month, one year’s worth of historical forecast-to-actual comparisons provides a relatively unreliable 12 deviation values, and even a one-week forecast period provides only 52 values. Historical daily demand variation based on customer-requested fulfillment, not forecast-to-actual-demand forecast error, provides the best indicator of potential service-level failures.
Even if all of the assumptions on which Formula (1) and similar formulas are based were satisfied, we contend that these formulas are not “correct,” in part because they optimize the wrong service-level criterion. These formulas aim to limit the risk of a stockout occurring over a lead-time period. This is an event-oriented criterion. This is not how service level is measured at most companies. Most companies measure service level as a fill rate (see http://en.wikipedia.org/wiki/Service_level), where the “beta” and “gamma” criteria are described).
We have developed a safety-stock approach that is fill-rate based. Beyond this, it integrates the many other parameters that affect inventory levels and thus safety stock. Our approach is correct and comprehensive, in contrast to the many simple formulas that are available. For example:
None of the safety-stock formulas you cited provide a confidence interval, or range of possible results based on the variation of all the variables. Instead, the implied confidence of these formulas is only 50%. This means that even if the assumptions behind the formulas were satisfied, the safety-stock level itself would, on average, achieve the desired service level only 50% of the time. This low confidence would result in a financially-unfavorable combination of expediting and unhappy customers for one month, quarter or year out of every two, on average. Our safety-stock approach allows you to specify your desired confidence level (we suggest 90-95%).
All of the safety-stock formulas you cited assume that actual demand is normally distributed. Actual demand is often right-skewed and may also be quite sporadic. Actual demand has a natural lower bound of zero, but no upper bound. The upper range of a demand distribution poses the potential for service-level failures. Our safety-stock approach accommodates actual demand-distribution skewness and sporadicity.
Our approach adjusts safety-stock levels for positive or negative forecast bias, if your acquisition is driven by forecast (such as MRP).
Our approach also includes these factors that definitely affect safety stock and service levels: Historical daily demand patterns; quantity-based fill-rate targets; realistic lead times; MOQs / EOQs / package sizes / reorder-review intervals; probability of unfulfilled-demand cancellation; high confidence of consistently achieving fill-rate targets; expected near-future trend and/or seasonality.
I’ll be happy to perform our correct, comprehensive safety-stock analysis on up to 30 of your items as a free trial, just as I’ve offered at https://www.resourcesystemsconsulting.com/blog/blog (about the third posting down from the top).
See our white papers on safety stock at http://topdownleansystems.com/white.htm. Take the Safety Stock Quiz, at http://topdownleansystems.com/quiz.htm. Contact me at http://topdownleansystems.com/contact.php.
David McPhetrige, TopDown Lean Systems
Hello everyone.
A question about the following formula:
{Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}
Shouldn’t the correct one be {Z * SQRT (Avg. Lead Time ^2 * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2 + Standard Deviation of Demand ^2 * Standard Deviation of Lead Time ^2)}?
Also, has anyone studied the following variation:
{Z * SQRT (Avg. Lead Time ^2 * MAD ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2 + MAD ^2 * Standard Deviation of Lead Time ^2)}
Where MAD = (Sum(|Real Demand – Forecast|)/n) where n = periods
I’d really apreciate your comments.
Thanks
Kenneth,
First, your L(z) question about the Quick MBA service-level formula, which seeks to find a safety-stock quantity that provides a quantity-based, as opposed to a stockout-event-based, service level. This formula is based on the idea of computing the expected number of units late over a time period, given a distribution that represents the demand. In the Quick MBA formula, that time period is the lead time (l), adjusted by the reorder period (p).
This formula first requires your desired fill-rate service level, say f = 0.98. Next, let’s suppose your demand distribution is approximately normal, with mean = 50 and standard deviation = 10. Also, let’s say that the reorder period is 5 days, and that lead time is 2 days. Then L(z) = ((1 – 0.98)*50*5)/(10*(5+2)^.5) = 0.189.
Next, look up L(z) in a table of normal-loss-function values. The corresponding z-value is approximately 0.53. Take this value and multiply it by the standard deviation of demand times the adjusted lead time (the square root of the total period of 7 days): S = 0.53*10*7^.5 = 14.0, which implies that safety stock of about 14 units is needed to obtain a 98% fill rate.
This safety-stock calculation, based on the unit normal loss function, reflects a quantity-based service measure. In our example, we expect our demand quantity during lead time to be 100, and our quantity-based service level is 98%, so we would like to have sufficient safety stock to ensure that 98 of these are fulfilled on time. The Quick MBA formula uses L(z) to obtain a value that corresponds to the desired 98% fill rate.
In contrast to this calculation that finds a safety stock value intended to achieve a desired fill rate, formulas such as the one from Inventory Management Review seek to ensure a level of stockout (or no-stockout) events. So, you might calculate safety stock to ensure a 98% no-stockout rate. Note that the stockout could involve 4 items or 4000 items – this formula does not distinguish, it looks only at the probability that a stockout occurs.
One practical concern with the stockout-event approach is that it rarely represents the way you measure your actual service-level performance. For example, you may track actual demand quantities delivered on time as a percentage of total demand quantities, a typical “on-time delivery” measure. Likely, you also have a strategic target for this quantity-based on-time-delivery measure. Let’s say that your on-time-delivery target is 98%. If you use the Management Review formula for your calculation, you are actually determining the safety-stock level required to achieve 98% probability of no stockouts. This is very different from saying that 98% of the demand quantities will be on time.
Generally, event-based safety-stock formulas provide higher safety stock values than do fill-rate based formulas and methods. If your actual service-level performance measure is quantity-based, and your safety-stock level is based on the probability of no stockout events, your safety stock levels may be too high.
Both formulas we have discussed assume that total demand over the period of interest is approximately normal. In reality, demand data is rarely normally-distributed. It follows that the central limit theorem may not apply, especially when the lead time is short, the demand distribution is significantly skewed, and/or demand is sporadic.
Next, your question on demand-data intervals: From a practical perspective, daily demand data is best, for several reasons. 1) Usually, one wants to have safety stock to cover demand each day. This requires that the estimate of demand variability (standard deviation, for example) be based on daily demand data. If, say, the daily data are binned by week and the standard deviation of the weekly data is computed, this estimate will conceal variability that occurs on a daily basis, thus giving incorrect results when used in calculations. 2) Trends, seasonality, other patterns and special causes can be concealed by weekly or monthly data. With short product life cycles and market volatility, your representative historical demand-data time frame may be only 12-24 months. If this data is in weekly or monthly bins, you will have only 52-104 weekly, or 12-24 monthly, data points. By contrast, daily data will provide you with several hundred data points.
Finally, your question on “beta”: As Lawrence Loucka indicates in his posting dated September 11, 2009, beta is intended to adjust lead time for forecast interval, and forecast interval for order cycle interval. I suggest you contact Kent Linford, the author of the formula, to get his explanation of beta.
Importantly, the Linford formula acknowledges that MOQ, EOQ or reorder-review interval can have a significant impact on the safety-stock level actually required to achieve a target service level. Intuitively, this makes sense: A large MOQ provides “de facto” safety stock, so that little or no additional calculated safety stock may be needed to achieve the target service level.
I’ll be happy to discuss these various safety-stock factors with you. The best way to contact me is on http://topdownleansystems.com/contact.php. Also, I’m the only “David McPhetrige” on Skype.
David McPhetrige, TopDown Lean Systems
Mojtaba,
Short answer: Since your demand data is in monthly intervals, and your lead-time is a whole-number-month multiple, be sure that all of the factors in your safety-stock calculation are expressed and/or calculated as monthly values.
Longer answer:
1. Monthly data may not offer very many data points, and statistical reliability will suffer. For instance, a year’s worth of demand data is only 12 points, and this is not a very good sample size for several reasons. For one thing, your standard deviation estimate will only reflect month-to-month variability, and this will most likely be smaller than the amount of variability that you would see in weekly or daily data. Keep in mind that you can run out of stock any time during a month, and using monthly buckets treats demand as if all that matters is whether it is late in that month. It does not distinguish whether a stock-out occurs early in the month or late in the month, since within-the-month variability is not acknowledged. Also, monthly values conceal interesting patterns that may occur during a month, for example, trending, cyclical effects, or simply high-volume periods. If there’s any way you can get daily or weekly demand data, you’ll have many more data points to work with, and more reliable results.
2. The formula you posted uses a normality-based z value. This assumes that your demand over lead time is approximately normally distributed. In reality, demand is typically right-skewed, and may also be sporadic, meaning that normality-based calculations may result in incorrect safety-stock levels.
3. Make sure your actual service-level-measurement criterion matches the criterion you use in your safety stock approach. (See the Wikipedia entry for “Service Level”.) Likely, you measure your actual service-level performance as a quantity-based fill rate, such as on-time delivery (demand quantity fulfilled on time / total demand quantity). By contrast, a typical z-table shows the cumulative probability of no stock-out events. This z value is a different service-level criterion than your actual, quantity-based measure.
4. The formula you posted suggests that service level, lead time, demand variation and lead time variation are the only factors that significantly affect safety stock. However, MOQ (or EOQ, or reorder-review interval) also affects safety stock. Additionally, past-due demand backlog can make a big difference in safety stock requirements. In contrast, your posted formula assumes that demand not fulfilled on time is canceled.
5. A comprehensive safety-stock approach should provide you with a range of safety-stock levels that reflect various likelihoods of achieving the service level you desire. The value that you select from that range should represent the confidence you need to have that the safety-stock level will consistently achieve your service-level target.
I have another post on this forum, “Safety Stock Optimization”, at http://resourcesystemsconsulting.com/blog/blog. As it says, we will provide a complete, comprehensive free trial safety-stock analysis on up to 30 of your inventory items.
David McPhetrige, TopDown Lean Systems
DEAR ALL
I HAVE QUESTION ABOUT THIS FORMULA {Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}.
WE HAVE MONTHLY DEMAND & LEAD TIME IS 3 MONTH ACCORDING TO THIS INFORMATION HOW WE CAN USE THIS FORMULE
Fill rate and customer service levels mean the same thing.
Whatever time bucket you use, just be consistent. If you have lead time in days and demand in months, the math will be wrong.
For your question on Beta, why not write to Kent Linford(kent.linford@moen.com)?
Hi, I’m here again.
I’m trying to calculate the safety stock (see formulas on top of this page) but this really doesn’t work for me.
For calculating L(z), what do they mean with desired fill rate? Is this the same as the customer service level?? And what do they mean with the demand (daily, weekly, yearly)??? When I calculate this, I calculate that L(z) = 497. But is this possible because the table only goes until 3,09.
And then I calculated the formula from Apics but this formula doesn’t work either. What do they mean with this “beta” (between 0,5 and 0,7). What do Which beta da I have to use?
Can someone please help me with this problem?
Thanks everyone
Paw,
Please forgive me for answering your question with more questions. Might I ask for some clarification, please:
On this 25% of orders that are known, do you have enough visibility of demand (the customer allows you enough lead time) so that you can acquire (make or buy) what you need to fulfill this demand “to order”, instead of from stock? If this is true, do you actually acquire this 25% of demand “to order”, or allocate/reserve inventory for this demand as soon as the demand is visible, so that the inventory is unavailable for other orders?
What is the time interval for your historical demand data that you’re using in your estimation of standard deviation? Daily, weekly, monthly…?
I don’t understand the logic for adding R (replenishment interval), converted to weeks, to your lead-time days, and then taking the square root of that total. Could you explain this, please? As a general rule, longer replenishment intervals require less safety stock than do shorter intervals. This is because the larger reorder quantity, which is driven by the longer replenishment interval, provides some degree of “de facto” safety stock. By contrast, the formula in your post indicates that a longer replenishment interval effectively increases lead time, and therefore also makes the resulting safety-stock level higher.
Is your z value of 2.326 intended to represent a 99% service level? If so, how do you measure your actual service-level performance? If your actual measure is a quantity-based fill rate, such as units delivered on time as a percentage of total units (on-time delivery), then your z value causes a mismatch between the calculation’s event-based probability of no stockouts and your actual quantity-based measure.
Is your historical demand data actually normally distributed? In my experience, demand data is often significantly right-skewed, and is also often sporadic. If this is true of your data, and especially with a five-day lead time, then you cannot depend on the central limit theorem to justify using a normality-based z value.
Thanks!
David McPhetrige, TopDown Lean Systems
Hi,
I wonder if I can reduce safety stock (SS), when fx. 25% of future orders (purchased orders) are known? As I see it these 25% don’t represent any variation, and it would make sence to be able to reduce SS corresponding to this. But how do I take known orders out of the calculation for SS? Can I reduce StDev some way?
A bit information to my data:
– My ERP is SAP R/3
– I have fixed replenishment periods R (½, 1 and 2 weeks depending on which warehouse)
– StDev on demand is calculated on 6 months of historical data
– z is fixed to 2.326
– Leadtime is 5 days for the 2 week replenishment periods (LT is considered fixed)
– The formula I use for SS = StDev * z * sqrt(LT+R/HistoricalDataInterval)(5workingdayweek)
(ex. SS = 100 EA * 2.326 * sqrt(5+10/5) = 403 EA )
/kind regards, Paw
Paw, first thought is to segment your demand, that is split the 25% known from the 75% variable demand and recalculate your mean and standard deviation. Then only carry safety stock for the 75%. But you will want to ‘protect’ your stable 25%. Might need to allocate inventory, or set a priority rule so that the 25% always gets ‘first pick’. When you split the demand stream you might want to check to see just how stable the 25% really is. Even booked orders can change in quantity and timing. Regards, Larry
Zuzana,
Thanks for your feedback on my previous reply and on my white papers. I must admit, those white papers are pretty detailed! Let me try to clarify the information that we require for our TopDown Lean Systems modeling approach. Really, we need only the following:
1. Demand values for each item over time (daily is best, as you discovered)
2. Lead time for each item (usually an average or representative value – see below)
3. Target fill-rate service level and its measurement period (often a quarter or year)
4. Reorder quantity (or reorder-review frequency)
5. Package size (or order multiple)
6. Probability of cancellation for demand not fulfilled on time
Requirement 3 comes from your company’s strategies, policies or performance measures. Requirements 4 and 5 come from your MRP/ERP/business system. Requirement 6 is usually 100% if you often have past-due backlog, or 0% if you are in a pure-commodity market. These values enable our model to calculate and integrate the many factors that affect safety stock.
As many experts have observed, calculating valid safety stock levels is not simple. The simple safety-stock calculations can provide unreliable results. Because I was never able to find a safety-stock formula that addressed all of the factors I listed above, my company developed our own correct, comprehensive safety-stock modeling approach. This approach draws on over fifteen years of experience, utilizes compelling statistical methodology, and has been subjected to extensive testing.
If you would like to provide data on up to 30 on your inventory items, I would be honored to provide you with correct safety stock levels as a free trial. I’ll provide detailed information on our data requirements, and I’ll send you an Excel file containing data examples.
See my “Safety Stock Optimization” forum at https://www.resourcesystemsconsulting.com/blog/blog.
The best way to send me your contact information is at http://www.topdownleansystems.com/contact.php. Also, my direct phone number is listed there, if you would prefer to call. If you’re on Skype, you may look me up in the directory. I’m the only “David McPhetrige”, and my time zone is CEST -08:00. Feel free to contact me at your convenience.
As for your lead-time variation, can you first tell me if, for a given item, the lead time varies significantly over time? If so, do you have detailed data on this variation? If you do, then please send us that lead time data along with the demand data for the 30 items that we will evaluate. This will enable our analysts to choose the best technique for handling the lead time variation. Otherwise, for each item, if there is only slight variation in lead time, as is often the case, an estimate of average or typical lead time is sufficient.
David McPhetrige, TopDown Lean Systems
Dear David,
Thank you for your replay.Now I know that I made a mistake by evaluating the consumption. I took the average consumtion per month..now I have the daily consumption figures and lead times. As far as I have material with diff. lead times I decided to split them in some groups, or maybe it will be better to evaluate ste std.deviation in lead time only based on my filling, or the biggest diviation in lead time divided by 3.
I´ve checked your white papers, but I have to say that it´s too difficult for me. Does it means that I need to have all that figures ( actual Fill rate, Averadge reorder point…)to calculate the safety stock?
Michelle,
Great point –- the simpler the solution to a problem, the better. As your post highlights, a fundamental goal of safety stock is to take care of the customer by addressing the difference between average demand and peak demand during lead time. Your basic formula also correctly emphasizes that both calculated and actual service levels should be based on quantities (as opposed to stockout events).
Often, more involved solutions are needed because safety stock also affects nearly every aspect of financial performance. This business reality means that the costs, expenses, warehouses and cash required for 100% service level are usually prohibitive. So something less than 100% service level is better for profit, but too much less than 100% can be disastrous. Determining the safety-stock level that maximizes financial results, and not just service level, introduces more complexity to finding the optimal difference between average demand and peak during lead time. (Really, the key is to determine the peak demand that we’re willing to cover with safety stock.)
Over 20,000 times per month, people make Google searches related to “safety stock.” In part, this indicates the challenges and frustrations of defining the optimal difference between average and peak demand during lead time. Here are two examples:
1. Intuition tells us that if an item has a large MOQ, it may not need any formal safety stock as an adder to ROP, gross requirements or other replenishment techniques. If we were to use a simple safety-stock approach for this large-MOQ item, ignoring the de facto safety stock effects of MOQ, we would calculate formal safety stock that would increase our inventory levels, tie up cash unnecessarily and reduce financial performance in general. To optimize financial performance, safety stock must consider the effects of MOQ, EOQ, reorder-review frequency and similar replenishment-interval factors.
2. Historical demand is not a perfect picture of future demand. History provides, at best, a probability spectrum of future demand. On the one hand, using the historical peak may overstate optimal safety stock for our desired service level. On the other hand, the probability of future peaks exceeding the historical peak may be considerable, and we may need safety stock exceeding the historical peak. We simply don’t know unless we “do the math.” We must make an informed business choice of the point along that future-demand spectrum that optimizes the balance of service-level benefits and inventory-related costs. Optimal safety stock requires a correct statistical approach.
The good news is that computers quickly crunch the mathematical and statistical complexities required for optimal safety stock. Our challenge, then, is to find and use a safety-stock model that has just enough complexity to give us the right answer. Personally, I’ve spent over 15 years developing my model. Your suggested basic calculation is always my “sanity check” whenever I get mired in the complexities that optimal safety stock requires.
Dave McP, TopDown Lean Systems
i know a simple formula for safety stock…and that is maximum usage during the lead time-normal usage during the lead time
Zuzana,
It would be my privilege to analyze a few samples of your data, if you would like. I’m the founder of TopDown Lean Systems. I have a correct, comprehensive safety-stock model that addresses random demand variation.
My model first identifies potential issues in the daily historical time-series data itself: trend, seasonality and outliers. Once any input-data issues are resolved, my model then determines safety stock (expressed in both quantity and days) to achieve a target fill rate with a high degree of confidence.
My comprehensive model requires six inputs for each inventory item (in addition to the item’s identifier / part number):
(1) Time-series demand data, daily if possible, at least one year’s worth if possible, even more is better if available;
(2) Target fill-rate service level;
(3) Typical, not necessarily average, lead time;
(4) The reorder quantity (usually MOQ or EOQ) and package size that drive replenishment interval;
(5) Number of business days in your actual service-level-measurement cycle, for example 90 days if actual service-level performance is for a quarter, so that your items’ actual performance and my model’s results use comparable time frames;
(6) Probability that unfulfilled demand will be canceled, a value of 0% if unfulfilled demand becomes past-due and is fulfilled late, or 100% if demand not fulfilled on time is canceled.
I can send you an input-data file with some data examples in it. Feel free to provide me with your contact info, http://topdownleansystems.com/contact.php.
For an example of my safety-stock-analysis outputs, see page 16 of my white paper at http://topdownleansystems.com/wpss.pdf.
Hi Kenneth,
I´ve used this formula.
{Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}.
But but when I took the average daily demand, the safety stock are too low…
Let me see your data. Send me a few samples. lmloucka@comcast.net
Kenneth,
Thanks so much for the feedback on my website link. (I’m glad it’s now working for you!) Also, I truly appreciate your opinion of my website and its content.
Dear Lawrence, thank you very much for your replay.
As far as I don´t have a forecast and the actual daily demand is changing I have to use historical consumtion to calculate the safety stock.
Should I take then the daily consumtion multiplied by the lead time ( a have diff lead times for diff codes) to calculate the avg.demand?
Because when I did it like that the values of safety stocks were low…
Thanks.
Just take the average of the daily demand (sum the daily divided by the number of days).
Zuzana, which formula have you used for calculating your safetystock??
Dear Lawrence,
I have got one question regarding the safety stock formula.
I´ve done the calculation, but the safety stock are quite high. I think that the problem is that I have the lead time in days and the consumtion is per month.
Is there any standard which can I use?
Thank you.
Zuzana, You must use the same units of measure. If lead time is in days then calculate the averaged daily demand (monthly demand divided by 20 for example). Better would eb to look at the actual daily demand.
A few days ago I tried your website (with the link above) but it didn’t work on my computer. Today, I tried again and it worked great.
Thanks for the link and by the way, great website!!
Kenneth,
I have developed a correct, comprehensive safety-stock analysis for random demand/usage variation. It determines the safety stock required to achieve a target fill rate at a confidence level. For details, take a look at my white papers: topdownleansystems.com/white.htm. (See also my previous posted reply to Susan Hallman-Shumaker.)
Oh now I see, thanks Lawrence.
I will save this table, than I can always consult it.
Anyone who has another formula for calculating Safety stock??
Thanks
Z table, also known as the Standard Normal distribution.
http://www.sjsu.edu/faculty/gerstman/EpiInfo/z-table.htm
http://en.wikipedia.org/wiki/Standard_score
also MS Excel can give you the values.
Here’s an abbreviated table:
Service Level and z value
.90 1.282
.91 1.340
.92 1.405
.93 1.474
.94 1.555
.95 1.645
.96 1.751
.97 1.881
.98 2.054
.99 2.327
Thanks Lawrence for the formula. There are a lot of formulas who use “Z”. Where can I find this Number, or how can I calculate it??
Safety Stock:
{Z * SQRT (Avg. Lead Time * Standard Deviation of Demand ^2 + Avg. Demand ^2 * Standard Deviation of Lead Time ^2}.
Hello,
I am a student Logistics Management from Belgium and I a have a question. I need to find a good formula for safety stock. A formula which pays attention to variable leadtime and variable demand.
Is there anyone who has a good suggestion??
Kind regards, Kenneth
Susan,
I have developed a correct, comprehensive safety-stock analysis for random demand/usage variation. It determines the safety stock required to achieve a target fill rate at a confidence level. For details, take a look at my white papers: topdownleansystems.com/white.htm.
what should be the formaula to calculate safety stock for flexible production systems?
what do you mean by ‘flexible production system’? For companies that make to order you may not need finished good safety stock. When well linked to suppliers with quick response and pull techniques you may not need raw material safety stock. Having no safety stock anywhere in a supply chain is rare and probably foolish.
What should be the formuala to calculte the safety lavaels?
Safety levels aren’t calculated, they are a management decision. The higher the level the lower the risk of ‘stocking out’, but also the higher the inventory cost. You could do an optimization: cost of lost sale verses inventory cost, but can you really know the true costs of poor customer service?
Susan,
A book for your consideration: Inventory Management Explained, by David J. Piasecki.
Feel free to write to me directly at lmloucka@comcast.net
I am looking for a LSS focused formula for calculating specific inventory level for achieved a desired fill rate. Not sure if the above is what I need. For a given location inventory I know what items are stocked, which items moved and how much, how those items moved (ie: straight from inventory, bought out, fill rate, etc…) and based on individual item inventory stratification classification I can segregate “good” boyouts from “bad” buyouts. I also know the overall fill rate for the location. What I am looking for is a calculation incorporating these (and other?) variables in order to state “In order to achieve desired fill rate of X% – I need to carry Y Inventory ($). I am beginning to feel like I am searching for the Holy Grail. Anyone have any suggestions?
Thanks,
Susan
Sean, from the article by Kent Linford … An element of this lead time adjustment is a variable called beta. This variable is used as an exponent in the adjustment. Most literature, including APICS
curriculum, recommends a beta between .5 and .7.
Sorry, but I’ve never used this approach for setting safety stock. Perhaps you could write to the author.
What is beta?
Is it some statistical distribution?
What is the difference between Saifty stock and minimum control inventory level?
Hamidur Rahman, the difference is that safety stock is generally considered a quantity, that is a number of units, while a control level is used as an action point or reorder point. The number for both can be the same. Sometimes they are not, it depends on your system and how you determine replenishment; whether you are using reorder point, time-phased reorder point, MRP, kanban, rate-based. Often I will need to hold additional inventory in flow above the safety stock quantity to handle temporary demand for promotions, or product model change, or seasonality.
Thanks Artem.
Lawrence,
could you please check the source of APICS formula, it seems that standart demand(D) should be squared.
Thank you.